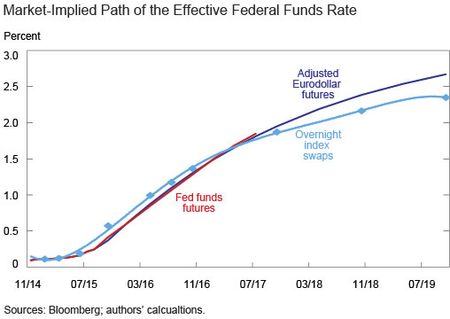
Market expectations of the path of future policy rates can have important implications for financial markets and the economy. Because interest rate derivatives enable market participants to hedge against or speculate on potential changes in various short-term U.S. interest rates, they are a rich and timely source of information on market expectations. In this post, we describe how information about market expectations can be derived from interest rate futures and forwards, focusing on three main instruments: federal funds futures, overnight index swaps (OIS), and Eurodollar futures. We also discuss how options on interest rate futures can be used to gain insight into the full distribution of rate expectations—information that cannot be gleaned from futures or forwards alone. In a forthcoming companion post, we explore an alternative source of policy rate expectations based on the two surveys conducted by the Trading Desk at the Federal Reserve Bank of New York.
Fed funds futures enable market participants to take a position in which the payoff is determined by the arithmetic average of the effective federal funds rate for a given contract month, and are a commonly used proxy for federal funds rate expectations. A number of academic papers (for example, Bernanke and Kuttner [2005]) have used changes in prices of fed funds futures to gauge the changes in rate expectations around economic or policy news releases. Fed funds futures contracts mature on the final business day of the delivery month, and are cash settled against the average daily effective federal funds rate for that month. In practice, the futures settle at 100 minus this average effective rate, so that an average rate of 50 basis points implies a settlement price of 99.5. While contracts trade on the Chicago Board of Trade for thirty-six calendar months, liquidity, as measured by open interest, tends to be concentrated in the first nine months.
An OIS is an agreement where one party pays a specified fixed interest rate (the “fixed leg”) in return for a floating interest rate payment (the “floating leg”) based on the geometric average of the daily effective federal funds rate over the contract period. The payoff on the fixed leg depends on the quoted rate at the time of the agreement and the realized effective federal funds rate, and as such OIS rates offer another measure of expectations for the effective federal funds rate. While fed funds futures trade on a calendar month basis, OIS are customizable, with contracts linked to the effective rate at various horizons, such as one week, three months, and one year.
Finally, Eurodollar futures permit investors to take a position on three-month Libor for given contract dates. Contracts are traded monthly out to six months and quarterly for ten years thereafter on the Chicago Mercantile Exchange. The payoff to Eurodollar futures is determined by the three-month Libor rate at contract expiry. This feature makes it necessary to adjust for the expected difference between three-month Libor and the effective federal funds rates when constructing a market-implied path of the future policy rate. In practice, the most straightforward way to make this adjustment is to use another set of derivative contacts, fed funds versus three-month Libor basis swaps, which are traded over-the-counter on forward dates from three months to thirty years. In these contracts, counterparties exchange the difference in interest accruals between the arithmetic average of the daily effective federal funds rate over the accrual period and three-month Libor as of the start of the accrual period. Given this structure, the quoted rate on the basis swap reflects expectations for the difference between three-month Libor and the daily average effective federal funds rate over the corresponding period.
Since the payoffs on all three derivative contracts we have discussed depend on the realized values for different short-term interest rates, they embed market participants’ expectations for the policy rate. It is important, however, to keep in mind that the implied policy rates extracted from these derivatives reflect the means of the perceived distributions of outcomes for the underlying rate, and as such are affected by the probabilities placed on rate outcomes away from the mean. Furthermore, they don’t purely reflect expectations because they also include a term premium component, which is the compensation investors require for bearing the risk that interest rates do not evolve as expected. Thus, movements in these market-implied interest rate paths could reflect changes in expectations for U.S. monetary policy, changes in the compensation investors require for bearing risk, or both. Disentangling expectations from risk premiums requires the use of a model of the behavior of interest rates and investors’ attitudes toward risk (see this previous blog post on Treasury Term Premia: 1961-Present for an example applied to the U.S. Treasury market).
Nevertheless, paths of the policy rate constructed from fed funds futures, OIS, and Eurodollar futures are useful tools to analyze market expectations. As shown in the chart below, as of November 28, paths derived from each suggest similar trajectories for the policy rate over the next five years.
What can we learn from options?
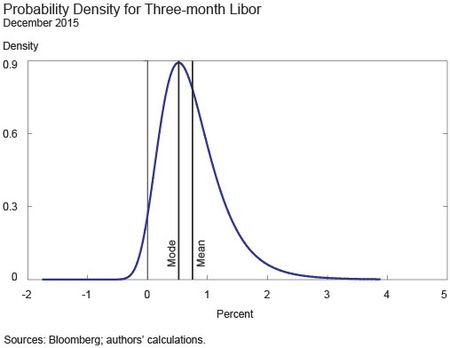
As noted, the market-implied paths presented in the above chart represent the mean of the expected future distribution of the policy rate. In order to get insight into the full distribution of expectations, we can use interest rate options. These options allow investors to lock in the right to buy or sell a futures contract at a pre-specified price (strike) and future date (maturity). By looking at the price of options across strike and maturity pairs we can recover an option-implied distribution. Armed with the whole distribution, we can calculate other measures of central tendency, such as the mode, and characterize the uncertainty surrounding market expectations.
Options on Eurodollar futures, in particular, are useful as they are traded frequently and have a wide variety of strikes and maturities. Using the Breeden and Litzenberger method, the next chart shows the option-based probability distribution for the three-month Libor rate as of December 2015 using Eurodollar option prices on November 28, 2014. The area under the curve over any interval represents the probability that market participants assign to the three-month Libor rate falling within that range in December 2015. The mean value of this distribution is equal to the rate implied by the Eurodollar futures contract.
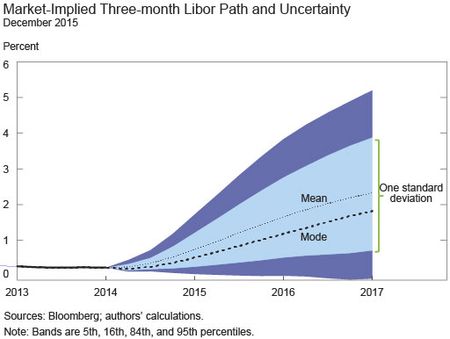
By combining probability densities for interest rates at different points in time, we can examine how investors believe interest rates could evolve over a number of years. For instance, based on data for November 28, 2014, the chart below shows the two measures of central tendency noted above (the mean and the mode) and roughly one and two standard deviations around the mean. This chart highlights the considerable uncertainty about the path of future short-term interest rates, especially after 2015.
Similar to the market-implied paths of the fed funds rate discussed above, there are a few things to keep in mind regarding the interpretation of these option-implied probabilities. First, option prices also embed risk premiums reflecting the required compensation for the risk that prices of the underlying contract do not evolve as expected. Second, the derived probability densities pertain to the future three-month Libor rate, rather than the effective federal funds rate. As a result, changes in the distribution may also be driven by factors that shift the expected basis between these two rates, including changes in perceived future credit risk associated with the Libor panel.
While interest rate derivatives have the significant advantage of being observed very frequently, they need to be interpreted with caution for the reasons discussed in this post. Instead of inferring the expected path of short-term interest rates from market prices, one can alternatively ask selected market participants about their rate expectations. We discuss this approach further in our companion post.
Disclaimer
The views expressed in this post are those of the authors and do not necessarily reflect the position of the Federal Reserve Bank of New York or the Federal Reserve System. Any errors or omissions are the responsibility of the authors.

Richard K. Crump is a research officer in the Federal Reserve Bank of New York’s Research and Statistics Group.

Emanuel Moench is a research officer in the Bank’s Research and Statistics Group.

William O’Boyle is a financial markets analyst in the Bank’s Markets Group.

Matthew Raskin is an assistant vice president in the Markets Group.

Carlo Rosa is a senior economist in the Markets Group.











 RSS Feed
RSS Feed Follow Liberty Street Economics
Follow Liberty Street Economics
I wrote this yesterday in response to someone on a blog related to Chinese financial markets… I think it is even more appropriate here. “I personally think if you don’t understand Black-Scholes you can’t understand price. Most people see price in the market as a static number and not as a center point of a distribution. If you learn to see the distribution you realize that the market is speaking in uncertainty and it is telling you that right up front. Otherwise you are reading an instruction guide that is missing every other page. No fault but your own, the info is there.”
STAN JONAS I’m puzzled by your assertion that ” option prices also embed risk premiums reflecting the required compensation for the risk that prices of the underlying contract do not evolve as expected”. Isn’t that exactly what you are interested in? The price of the option… or more precisely the price of a call spread or a butterfly is exactly representative of the markets implied probability that the price of the underlying ends up at certain price. Saying that you might be wrong in your probability assesment because prices of the underlying do not evolve as expected is clearly just a tautology. Stan Jonas