Thomas Piketty’s 2014 book Capital in the Twenty-First Century may have been a greater sensation upon publication than Karl Marx’s nineteenth-century Das Kapital. It made the New York Times bestseller list, generated myriad reviews and responses from economists at top institutions, and was the subject of a standing-room-only session at the recent American Economic Association annual meeting. In Capital, Piketty argues that wealth inequality is set to rise from its relatively low levels in the 1950s through the 1970s to the very high levels it once occupied at the dawn of the Industrial Revolution—the time of the heroes of Jane Austen and Honoré de Balzac. He supports this argument with voluminous evidence on the history of the capital stock and of inequality in developed countries, which he argues have been moving in ways consistent with his theory. Piketty proposes that governments worldwide intervene to prevent this rise in inequality, most importantly by levying a global tax on capital.
In this series, I will describe the arguments that Piketty makes to conclude that wealth inequality will rise and that global capital taxation is needed to stop it, and present a critical discussion of these arguments. My analysis starts with Piketty’s most famous formula, r > g.
What is r > g?
The main argument in Capital for why wealth inequality is set to rise comes from a simple relation: r > g. This formula states that the net rate of return to capital (r) exceeds the growth rate of output (g). This is not a new concept for economists. The formula r > g is a standard property of efficient capital markets in most modern macroeconomic models. (In fact, the converse, r < g, would imply that the economy is saving too much, and that it would be possible to increase the consumption of every person at every point in time by decreasing the capital stock and raising the interest rate at least to r = g.) However, r > g may be a strong amplification mechanism for inequality within the economy. In theory, if a capital owner invested one unit of capital, got a riskless return r on it every year, and reinvested this return completely (without consuming any of the capital or giving it away to her heirs), while a worker started out with a wage equal to one unit, which she consumed entirely but which grew at g percent per year, the ratio of the capitalist’s wealth to the worker’s wage would grow at the rate r – g. In practice, of course, capitalists face risk, split their fortunes among descendants, and consume at least some fraction of their wealth. However, Piketty shows mathematically in one of his papers that as long as capital can be accumulated for any period of time, and as long as there is some source of wealth inequality in the economy, wealth inequality must be increasing as the difference r – g grows. Note that for Piketty, r > g implies that the process of saving and investment (and, possibly, inheritance) acts as an amplification mechanism for existing inequalities, including labor income inequalities.
What’s happening to r – g?
Piketty makes his prediction that wealth inequality is set to rise based on analyzing the evolution of r and g over the course of human history. The chart below, taken from Capital, depicts this evolution. Piketty estimates that in an unregulated capital market in steady state, r has been about 4 percent to 5 percent historically since antiquity. Based on a variety of source documents, Piketty finds land price-to-rent ratios to have been around 20 or 25 in the days of ancient Rome, as well as in the preindustrial Britain described by Jane Austen. Currently, the price-to-rent ratio in many U.S. housing markets is also around this level. However, in the first half of the twentieth century, this rate of return was eroded by capital losses during the world wars, as well as by inflation, taxation, and regulation of capital, causing the effective value of r received by capital owners to plunge. Over the second half of the twentieth century, though, the value of r has recovered thanks to low inflation, and because countries, eager to attract mobile capital in a global market, have sought to decrease taxation and regulation to make themselves more investment friendly. Piketty assumes that this trend will continue into the twenty-first century, and r will return to its historic value of 4 percent to 5 percent.
As for g, Piketty argues that the growth rate of output has already seen its best days. Output growth is composed of two factors: population growth and economic growth. Piketty argues that population growth was zero for most of human history, soared during the industrial revolution, and is now declining (eventually to zero) as people control the sizes of their families. Economic growth, on the other hand, shall continue forever, but not at its current rates. Piketty’s main insight is that it is easier to copy than to invent; countries that are now relatively poor—like China, India, and the rest of the developing world—can grow at very high rates as long as they are poorer than the developed countries at the technological frontier (like those in Europe, the United States, and Japan). Currently, economic growth is at an all-time high because China and India are catching up to the developed world, but once they do, they will hit the technological frontier and grow much slower. Per capita economic growth in the world will, therefore, stabilize at the per capita growth rate of the countries at the technological frontier—the developed world—which for long periods of time has averaged approximately 1.5 percent per year.
What does this story imply about r – g? Before the twentieth century, r – g was on the order of 3.5 percent to 4.5 percent, which, Piketty calculates, was enough to sustain the very high wealth concentration of the preindustrial period. During the Industrial Revolution, r – g shrank, and during the twentieth century, which was a disastrous time for capital but a good one for growth, it actually turned negative for a period of time. However, Piketty’s projections imply that the gap r – g will open up once again. With demographic growth equal to zero, g will therefore be 1.5 percent, and with r returning to its long-run value of about 4.5 percent, the gap r – g will equal about 3 percent, a bit smaller than it was at the beginning of the Industrial Revolution, but still enough to maintain much larger inequalities than we saw in the twentieth century.
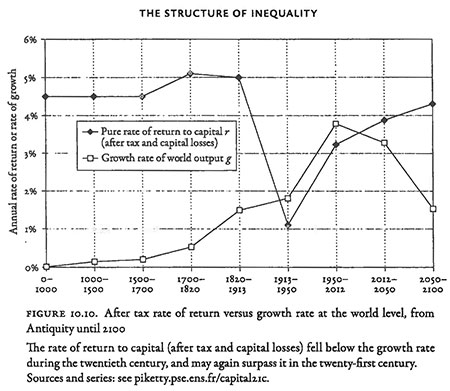
Note: We publish the chart verbatim from the original in Thomas Piketty, Capital in the Twenty-First Century (Cambridge: Harvard University Press, 2014).
Too Pessimistic a View of Growth?
Piketty’s crucial assumption underpinning his pessimistic view of growth is that the technological frontier naturally grows at a relatively modest 1.5 percent per year, since no developed country in the world has grown at a faster rate for a sustained period of time. But is the global technological frontier bound to grow no faster than 1.5 percent per year?
The chart below plots the logarithm of GDP per capita in the most advanced country in the world over the nineteenth and twentieth centuries. (It was Britain for the nineteenth century and the United States for the twentieth century, until the latter overtook the former as the country with the highest GDP per capita around 1900.) If GDP per capita were growing at a constant rate, the red line, which is the line of best fit for the nineteenth-century data, should have coincided with the twentieth-century data. Instead, we see that growth over the twentieth century in the economy at the technological frontier has been much higher than the constant-growth rate prediction based on the nineteenth-century trajectory, and the difference has been getting larger over time. In fact, modeling log GDP per capita as a quadratic (accelerating) function of time (the blue line) appears to fit the data much better, and to offer much better predictions for log GDP per capita in the twentieth century when the model is fit over
data for the nineteenth century. While the past path of growth at the frontier does not necessarily determine the future, the growth acceleration at the technological frontier over the course of the twentieth century shows that it is difficult to claim that economic growth rates will necessarily be as low over the next 100 years as Piketty believes.
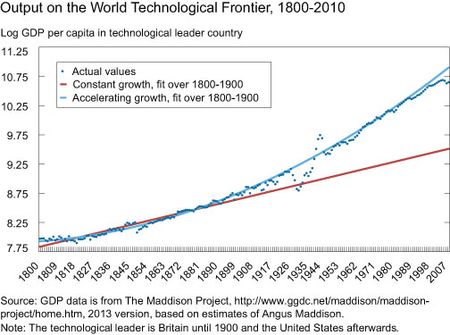
If growth rates at the technological frontier increase, then the difference r – g will decrease relative to Piketty’s prediction for the next century. If the trend captured by the blue (quadratic) line persists, then growth at the technological frontier in 2100 will be around 3.5 percent, reducing r – g to about 1 percent rather than the 3 percent that Piketty expects. Obviously, this is a big if—but so is virtually any other forecast made for the next century.
Disclaimer
The views expressed in this post are those of the author and do not necessarily reflect the position of the Federal Reserve Bank of New York or the Federal Reserve System. Any errors or omissions are the responsibility of the author.

Maxim L. Pinkovskiy is an economist in the Federal Reserve Bank of New York’s Research and Statistics Group.










 RSS Feed
RSS Feed Follow Liberty Street Economics
Follow Liberty Street Economics