Tobias Adrian, Richard K. Crump, Benjamin Mills, and Emanuel Moench
Treasury yields can be decomposed into two components: expectations of the future path of short-term Treasury yields and the Treasury term premium. The term premium is the compensation that investors require for bearing the risk that short-term Treasury yields do not evolve as they expected. Studying the term premium over a long time period allows us to investigate what has historically driven changes in Treasury yields. In this blog post, we estimate and analyze the Treasury term premium from 1961 to the present, and make these estimates available for download here.
The term premium estimates that we present are obtained from a five-factor, no-arbitrage term structure model. The model setup and estimation procedure are described in detail in Adrian, Crump and Moench (2013). Our model belongs to the affine class of term structure models which characterize yields as linear functions of a set of pricing factors. The model imposes no-arbitrage restrictions which ensure that the time series and cross section of bond yields are consistent with one another.
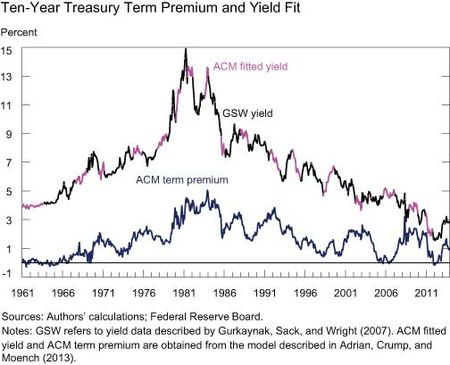
We estimate the model using zero-coupon yield data described by Gurkaynak, Sack, and Wright (2007), which are available at a daily frequency from the Board of Governors here. Fitting the full sample of yields allows us to estimate the term premium on a daily basis going back to June 14, 1961. The chart below compares the Adrian, Crump and Moench (ACM) model-implied ten-year yield to the ten-year yield of Gurkaynak, Sack, and Wright (GSW). The ACM model fits the data extremely well, allowing us to decompose yields without concerns about measurement error.
In a previous post, we compared our estimated term premium to a number of observable variables. We showed that the term premium is a countercyclical variable which tends to move with measures of uncertainty and disagreement about the future level of yields.
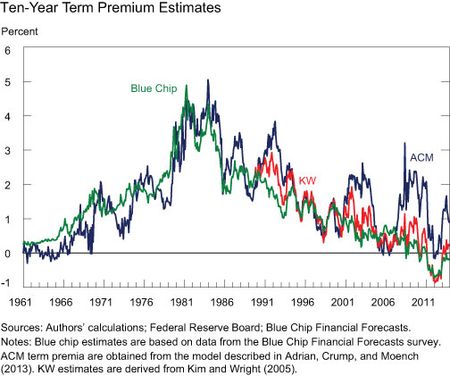
An alternative approach to estimating the ten-year term premium is to subtract the expected average level of short-term interest rates over the next ten years obtained from surveys of professional forecasters from the current ten-year Treasury yield. Unfortunately, longer-term survey forecasts are only available at a biannual frequency and only since the early 1980s using the Blue Chip Financial Forecasts survey (see these three posts for further information). However, by projecting this series onto the principal components of Treasury yields, we can construct an extrapolated monthly series that goes back to 1961. In the next chart, we plot this estimated term premium (Blue Chip) along with our estimate (ACM) and that of Kim and Wright (2005) (KW). The latter estimates the term premium incorporating some survey forecasts into a three-factor affine model. The chart shows that the different term premium estimates co-move at low frequencies but may differ markedly in certain periods. In particular, our estimate of the term premium has been considerably higher since the onset of the financial crisis than the other two series. That means that our model has implied a lower future path of short-term interest rates than those based on survey data.
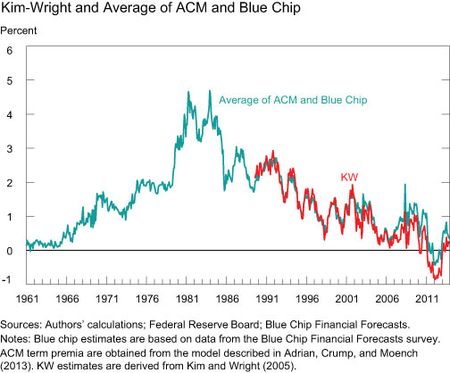
In fact, we can demonstrate the role of survey data in an even more transparent way by comparing KW to the simple average between our estimate and that purely based on surveys. The following chart shows that the KW term premium and this composite series are very similar.
The evolution of term premia has been of particular interest since the Federal Reserve began large-scale asset purchases. Over this time, short-term interest rates have been close to zero, and our estimates show that the term premium has been compressed and has at times even been negative. An advantage of our estimate is that it is available back to 1961. Hence, we can study the term premium at another time when short-term interest rates were close to zero. By comparing the ten-year ACM term premium of the past decade to that of the 1960s in the first chart, we find that the ten-year term premium was negative at times in the 1960s, but reverted back to positive. Similarly, our estimate of the term premium has risen above zero recently.
Daily estimates of the ACM term premium from 1961 to the present are now available for download from the Data & Indicators section of the New York Fed’s website. The data are updated weekly and include estimates of the term premium for yearly Treasury maturities from one to ten years, as well as fitted yields and the expected average level of short-term interest rates.
Disclaimer
The views expressed in this post are those of the authors and do not necessarily reflect the position of the Federal Reserve Bank of New York or the Federal Reserve System. Any errors or omissions are the responsibility of the authors.

Tobias Adrian is a senior vice president in the Federal Reserve Bank of New York’s Research and Statistics Group.

Richard K. Crump is a research officer in the Group.













 RSS Feed
RSS Feed Follow Liberty Street Economics
Follow Liberty Street Economics
An extremely interesting post. It is much appreciated that the data has been made available for general consumption and will be updated frequently. I note that your estimate of the level of the (ten-year) term premium is broadly in line with the long-run average and that which has prevailed since the early 1990s (when other Fed estimates seem to begin). This stands in contrast to the Kim & Wright measure, for instance, which would imply a still depressed term premium. Are you able to briefly sum up the intuition behind the divergent estimates? Material differences do appear to have emerged in recent years. Is there something in the nature of the constructed models that has driven these differences?
So does your work suggest that the term premium should rise as QE is reduced?
Thank you for your interest in our work. In regards to the relationship between large-scale asset purchases (LSAPs) and term premia, in separate work (http://www.newyorkfed.org/research/staff_reports/sr570.html), we find that LSAP announcements have primarily reduced longer term yields through a reduction of real term premia. Real term premia are the compensation investors require for bearing real interest rate risk, which is the risk that bond yields indexed for inflation do not evolve as expected.
Can you please translate your findings into layman’s terms, with particular emphasis on what your finding mean for current term yields? Obviuosly, there is a huge interest among market professionals in the topic of the degree to which QE did or did not “artificially” depress bond yields. Any light that your research can shine on that question would be of wide interest in the financial market. Thank you.
Thanks to the LSE readers who pointed out that the link to our Treasury term premia estimates was not working. The link has been restored and the data are now accessible.