Olivier Armantier
In finance, auctions are often conducted to buy or sell simultaneously various assets with very different characteristics. These auctions raise a number of challenges that cannot always be addressed with standard auction designs. In this post, I discuss an alternative design—the “reference price auction”—and present evidence that it may dominate other methods often implemented in practice.
Financial institutions often attempt to raise a specific amount of liquidity by auctioning (in a process sometimes called a BWIC, or “Bids Wanted in Competition”) the various assets of a failing institution, or a portfolio of, for instance, distinct mortgage-backed securities with different ratings or vintages. Conversely, procurement (reverse) auctions can be conducted to buy simultaneously various assets with different characteristics. For example, open market operations, the most common channel through which monetary policy is implemented around the world, can involve daily multi-billion-dollar auctions in which a central bank decides to purchase a fixed dollar amount of various securities from a set of eligible sellers. Likewise, in the fall of 2008 the U.S. Treasury contemplated running auctions to purchase a wide spectrum of “toxic assets” from troubled financial institutions.
The conduct of such auctions raises a number of challenges, including dimensionality (there may be a large number of very different assets), information asymmetry (one of the parties—for example, the sellers—may have more information about the value of the assets), concentration of ownership (one bidder may own most of one of the assets), and time constraints (the auction typically needs to be completed within a short period of time). In this context, one may wonder about the relative performance of different auction designs.
To illustrate, consider an institution that organizes a procurement auction to purchase a fixed dollar amount of various securities. It is common for the institution to hold a “grand auction,” whereby the securities with the lowest price bid are accepted first until the buyer’s budget is exhausted. An advantage of this approach is that it may promote competition by letting owners of different securities compete against each other. However, with low bids likely to come for the worst securities, the buyer is likely to end up purchasing the lowest-value securities and overpay, a phenomenon known as adverse selection.
To illustrate this phenomenon, consider a very simple example with two bidders (1 and 2) and two assets (A and B). Bidder 1 owns two units of asset A, while bidder 2 owns two units of asset B. Unlike the buyer, the bidders know that assets A and B are worth $20 and $80, respectively. Finally, say that the buyer has a budget of $100. In that case, a bid by bidder 1 of $50 per unit guarantees that his or her two units are accepted by the buyer (since bidder 2 is not willing to bid below $80). The buyer then ends up buying the lowest-value asset, and overpays (paying $100 for two units worth $40 in total). An alternative is to conduct a separate auction for each type of security. While this approach effectively deals with differences in the value of the various types of securities, it requires in part running many auctions, which is often considered impractical and undesirable.
In a recent paper by Armantier, Holt, and Plott, we present a different design, called a reference price auction. The basic idea of the design is that the buyer sets and publicly announces before the auction “reference prices” that reflect value estimates of the various securities in the auction relative to a baseline security. After receiving all bids, the buyer normalizes them by dividing the unit price bid for a security by the reference price corresponding to that security. As a result, the bids for different securities can be compared. In a simple illustration, the buyer would deem a security with a reference price of 2 to be twice as valuable as the baseline security. Bids on a security with a reference price of 2 would then be divided by 2 to make them comparable to bids on the baseline security. The normalization process would therefore lower the price bid for securities with higher reference prices and raise the price bid for securities with lower reference prices. The buyer would then accept the securities with the lowest normalized bid until his or her budget is exhausted.
We argue that the main benefit of this design is that it should create a level playing field by making the bids for securities of different values directly comparable. As a result, it should promote competition across bidders and assets, and it should provide some protection against the previously discussed concern of adverse selection. The performance of the auction, however, may rely heavily on the buyer’s ability to precisely estimate reference prices. In particular, bidders could potentially exploit valuation mistakes at the buyer’s expense. A possible remedy to mitigate such a problem could be for the buyer to reveal the reference prices only after the auction, so that the bidders would not be able to observe the valuation mistakes when they submit their bids.
To test the performance of the design, we conducted four laboratory experiments that simulate the environment with financially motivated human subjects. The first experiment is a grand auction, while the other three are reference price auctions. In the second experiment, the bidders know that the buyer is able to set reference prices with perfect accuracy. In the last two experiments, everyone knows that the buyer makes large mistakes when setting reference prices. In the third experiment, the inaccurate reference prices are announced to the bidders before the auction, while in the fourth they are kept secret until after the bids have been submitted.
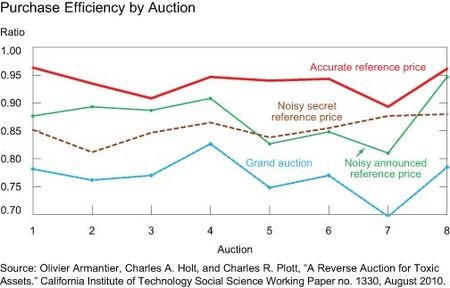
The main results of the experiments can be observed in the chart below, where the average purchase efficiency (that is, the ratio of the value of assets purchased to the buyer’s expenditure) is plotted for each of the eight auctions conducted in each experiment (note that the experiments were organized so that the efficiency ratio could not exceed 1). The grand auction produced an efficiency ratio of 0.76, meaning that for every dollar spent, the buyer purchased only seventy-six cents in value. In contrast, with an efficiency percentage ratio of 94 percent, the reference price auction is almost fully efficient when the reference prices are evaluated with perfect accuracy. The two experiments with inaccurate reference prices produce intermediate purchase efficiency ratios. This implies that, because of its homogenizing properties, a reference price auction remains superior to the grand auction—even when the buyer has very little information about the relative values of the securities. It is important to note, however, that keeping the inaccurate reference prices secret at the time of the auction, rather than announcing them before the auction, does not improve the auction’s efficiency. Our analysis reveals that the latter result is due to the fact that the auction with announced inaccurate reference prices creates sufficient competitive incentives to offset the incentives to exploit mispriced reference prices.
In summary, our results indicate that the reference price auctions clearly dominate the commonly implemented grand auction, even when reference prices are extremely inaccurate; but keeping reference prices secret before the auction does not improve performance. These results provide some support to the views of some auction designers who have argued that, beyond optimality considerations, the performance of an auction is mostly driven in practice by basic economic forces, such as finding simple ways to promote competition.
Disclaimer
The views expressed in this post are those of the author and do not necessarily reflect the position of the Federal Reserve Bank of New York or the Federal Reserve System. Any errors or omissions are the responsibility of the author.

Olivier Armantier is an assistant vice president in the New York Fed’s Research and
Statistics Group.










 RSS Feed
RSS Feed Follow Liberty Street Economics
Follow Liberty Street Economics